Page 21 - FitxesMatSols

Y Y 0 Y
−∞ ]

= = ∞
→ ( ) → [ ( ) Indeterminacions − ∞ Y 1
lim lim ∞
.
0 = → ∞
= a ∈ · 0
→ ( ) lim → ( ) ] =

lim +∞ ] _ = 2 −3
= `F ] ^ = = 2 = 1 =
→ ( ) lim lim →( _) \ ( ) lim →( _) = ( ) lim \ ( ) lim = ( )

Gràficament Funcions definides a trossos. Límits laterals ] ^ = ] _ = →f →f

→ [ V( ) → [ ℎ( )
−∞ lim lim

= = =
→ ( ) lim \ ( ) lim = ( )
.
0 = lim → [ → [
=
→ ( ) lim → ( )

lim +∞ Y * ≤ Y >
= lim → ( ) V( )WF U ℎ( )WF

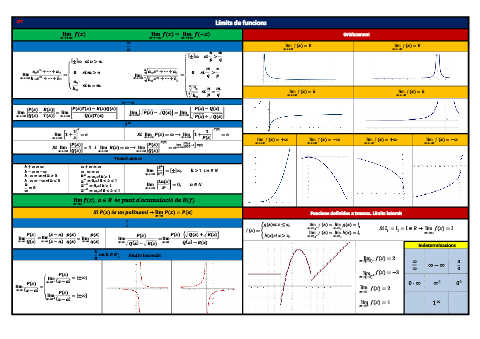
Límits de funcions = ( )

> - , > * , - = - , 0( ) − 1( ) 0( ) 9 : = H ∈
→ (− ) ±"∞ %& %& + %& + = → 5 +0( ) + +1( ) 6 → /9 + 0( ) 4 1 F ) > B J ∈ 1( ) − 2( )

, - 1( ) : →=> ? 0( ) 9@·2( ) 0( ) = 0( ) · b+1( ) + +2( )c

= = ⟶ ∞ = ±"∞, , = =
→ ( ) + + ⋯ + = 2( ) = 4 0( ) → →

→ + + ⋯ + → 7+0( ) − +1( )8 ;& → 0( ) 1( ) → / B → / I ( ) 4 2 é% ,L M N O PL LQ P&ó N: S( ) →

, - → / 0( ) 4 Qí &M% Q M:i Q%
0( ) +1( ) − +2( )
∞ − ∞ 9 ⟶ ∞ = Treball amb ∞ < 1 ;& 0( ) é% L ,TQ& T & → 2 ∗ ,

* 9 & → 2( ) < 1 ∈ B T B ∈
( ) = ∞, %& B > 1 = , %& < . = , %& B > 1 = ∞, %& < .
> > = = → 5 0( )3( ) − 2( )1( ) 6 1( )3( ) : ∞ + ∞ = ∞ ∞ · ∞ = ∞ ( ) , ,( ) → -( ) *
→ ( ) ±"∞ %& %& %& = 1( ) B B B B → = ±∞" = ±∞" =

= → /9 + 9 4 ;& → / 0( ) 4 = = ( − ) · ,( ) → ( − ) · -( ) 0( ) → \ ( − ) 0( ) → = ( − )
+ ⋯ + → + ⋯ + → / 0( ) − 2( ) 4 3( ) B − ∞ = −∞ B · ∞ = ∞ %& B > 0 B · ∞ = −∞ %& B < 0 =

1( ) B + ∞ = ∞ B ∞ = 0( ) → 1( ) 0( ) ( − )
∑k →